贝贝60秒:利乐柔性凸轮问题的新起点
曲政 / 2019-03-21
今天是贝贝报告给你的第 21 天
2019-03-21 星期四
八年前,我做利乐柔性机的电子凸轮曲线,没有成功。八年后,除了还不会用的工具,除了眼角的皱纹,有什么新东西支撑我的信心?
我有了新的数据。
虽然只是找到了一幅加速度的曲线图,但是我能读出以下信息:
- 相位功能——轭和爪在什么角度区间做什么动作,实现什么功能。以前我想得有偏差,少了一个功能。
- 曲线类型——用多项式还是用三角函数来定义各段的动作。以前我选得不好,加速度曲线不光滑。
- 峰值大小——每小时8000包的速度,可以容许多大的加速度。以前我不敢,故意压平了加速度曲线。
这张图是我的新基线。我会先用样条曲线拟合,把曲线信息数字化。然后,用恰当的函数定义加速度,两次积分生成速度和位移曲线。最后,争取做出动画模拟。
这张图可能也是我的极限。没有伺服电机实地测试,没有动力仿真验证性能,我最终只好用这张图,证明结果的有效程度。
蛋生鸡,鸡生蛋。这种验证有意义么?你有什么办法,欢迎留言给我。
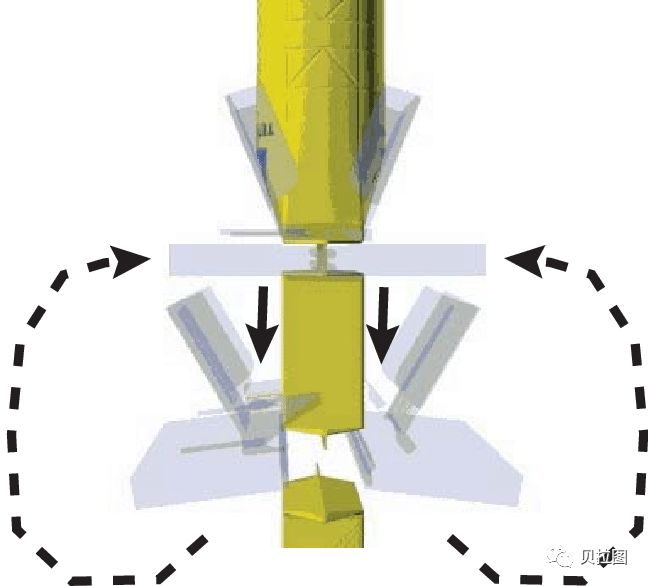
图 1: 利乐砖包成型动作示意
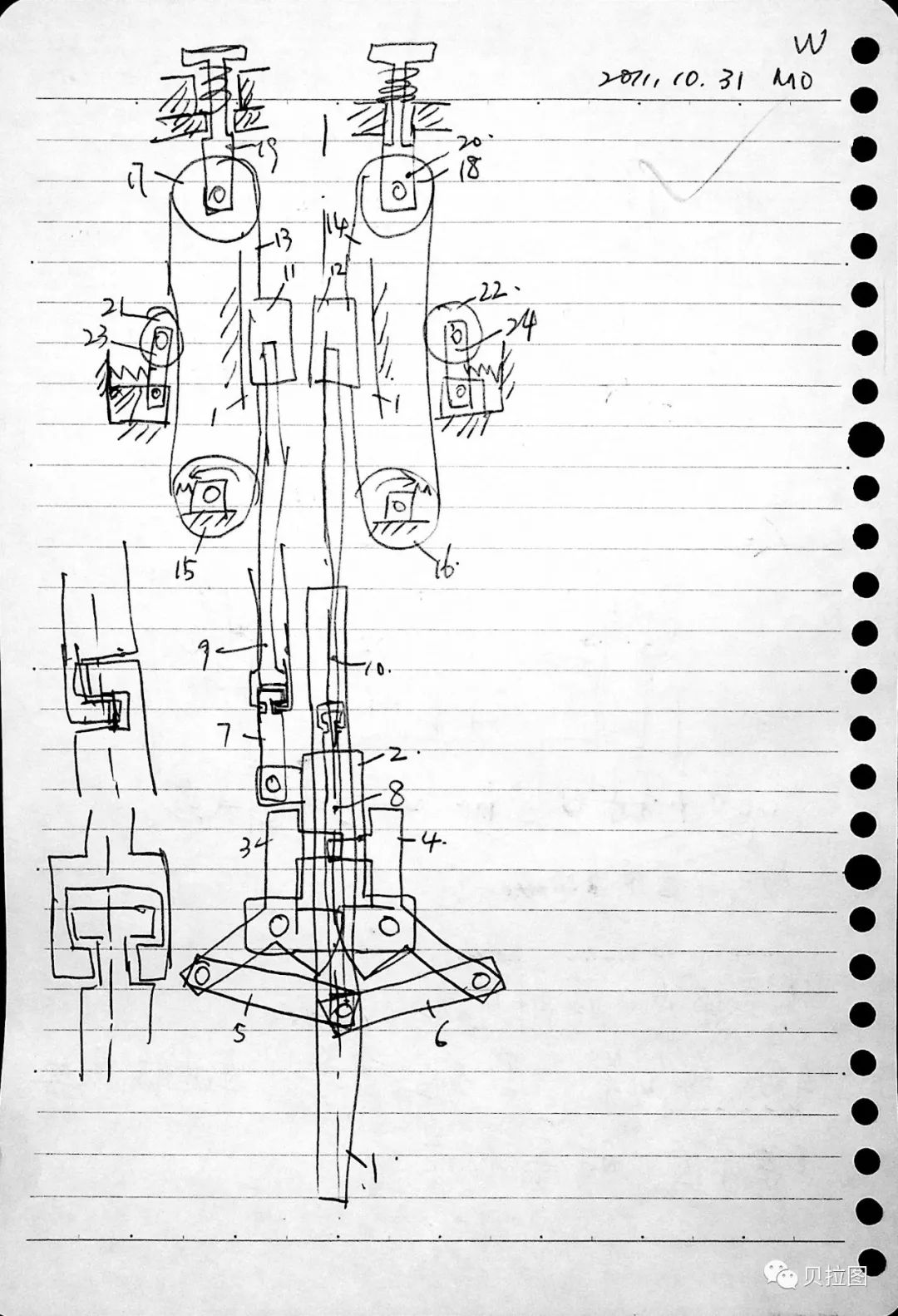
图 2: 利乐柔性机轭和爪的机构示意
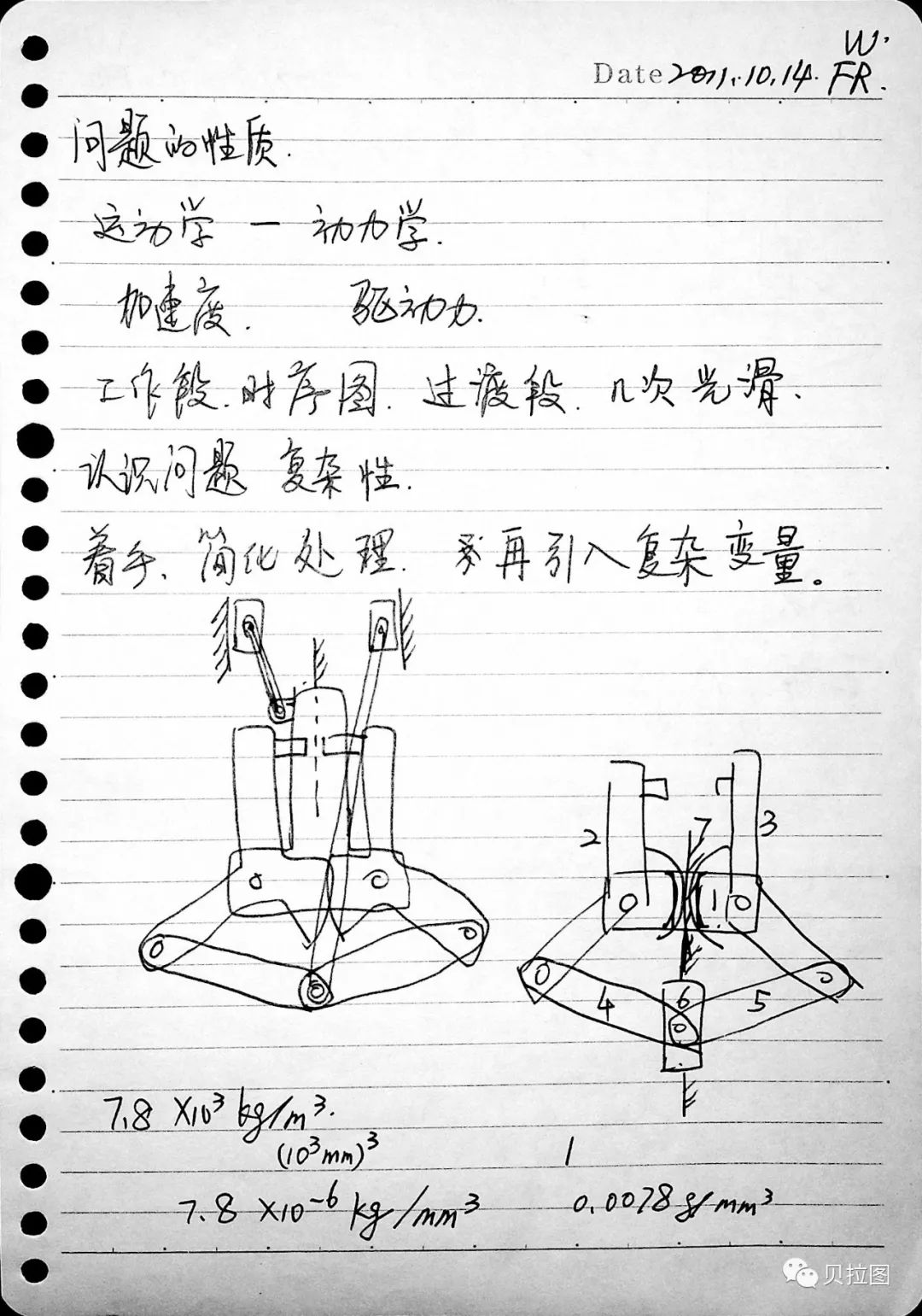
图 3:当年我对问题性质的理解
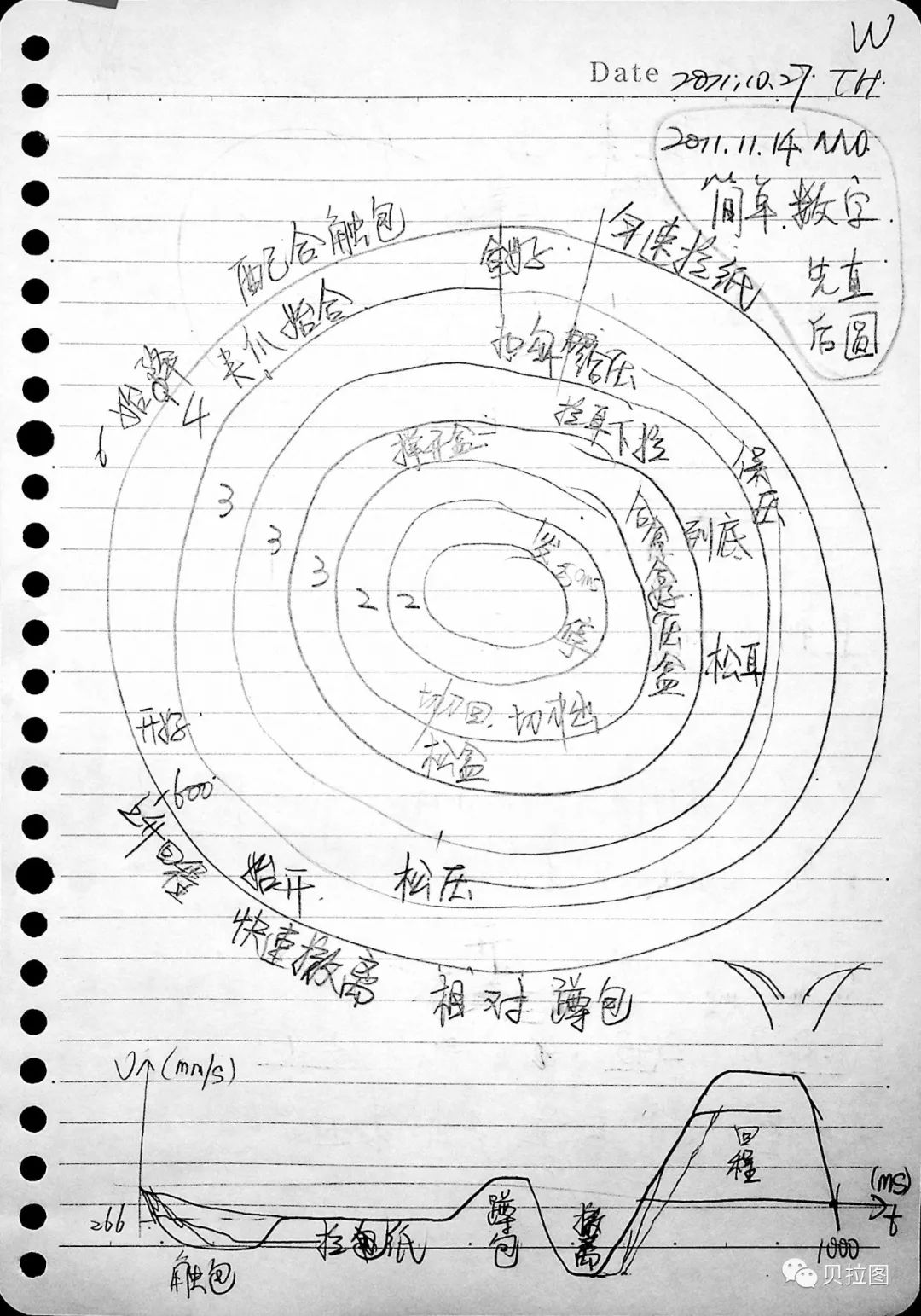
图 4:当年我对相位功能的理解

图 5:当年的我决定不用商业软件
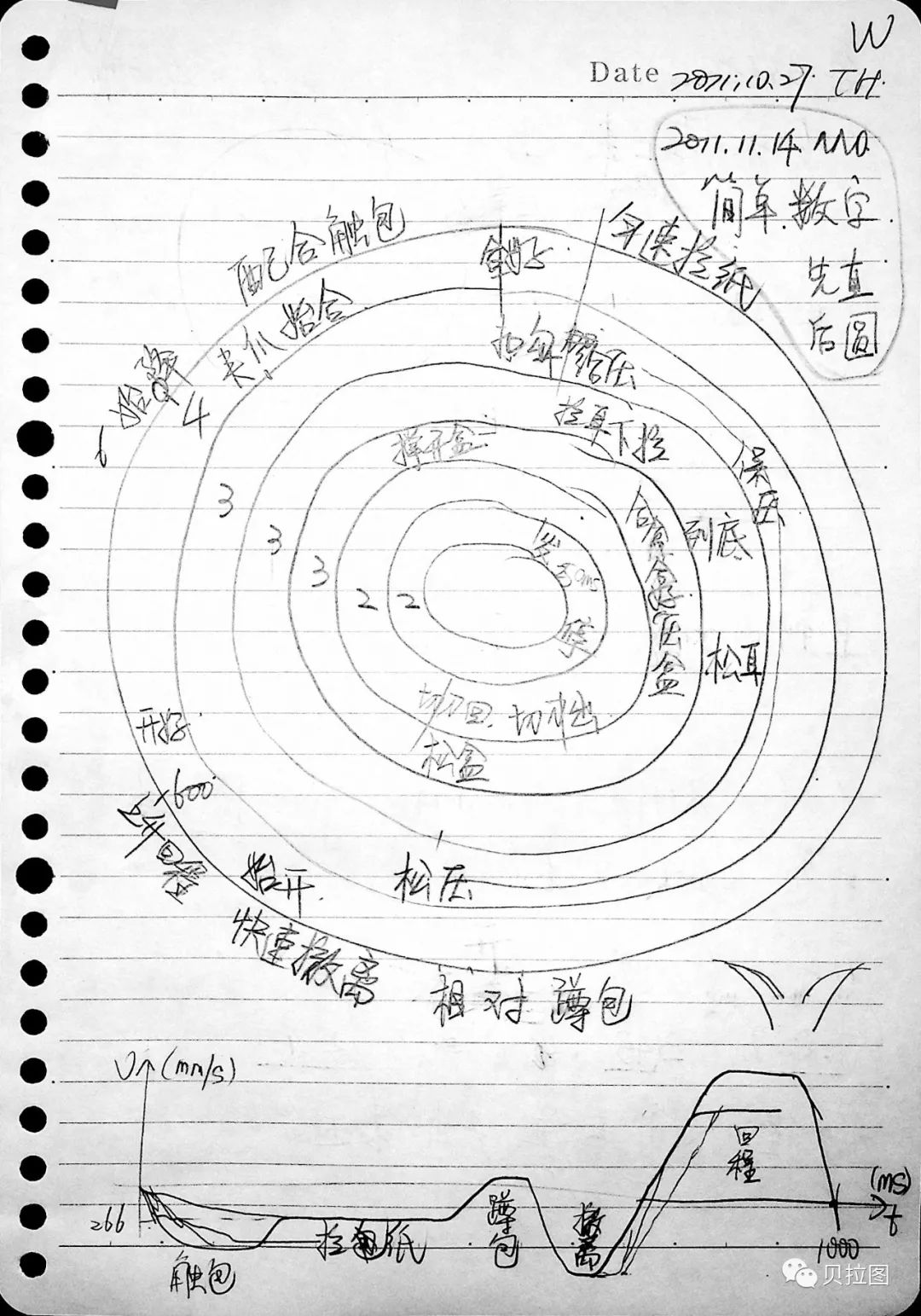
图 6:当年我对动作的定性理解
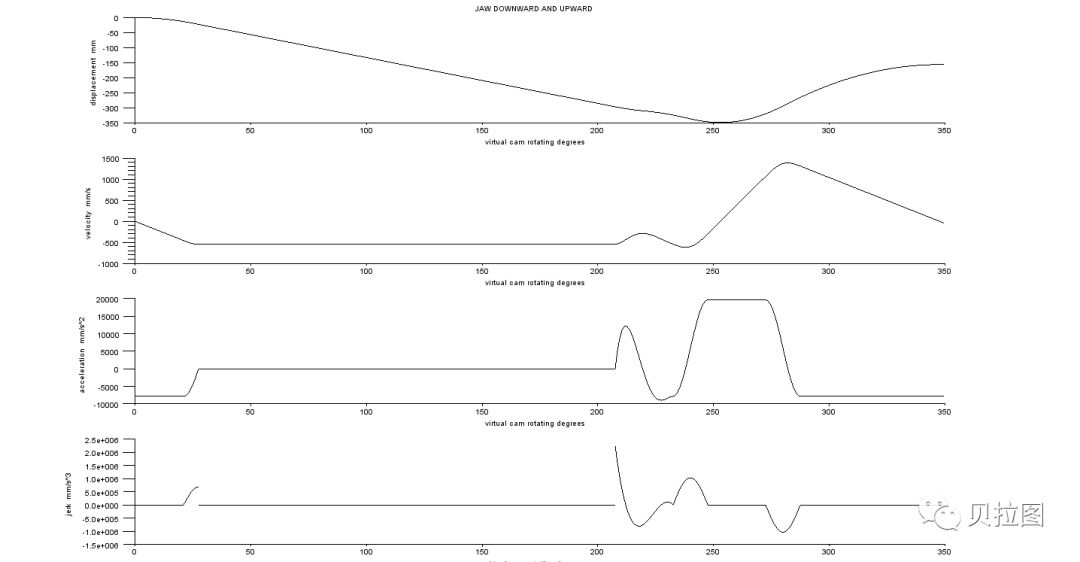
图 7:当年我用 Scilab 算的 s v a j 曲线
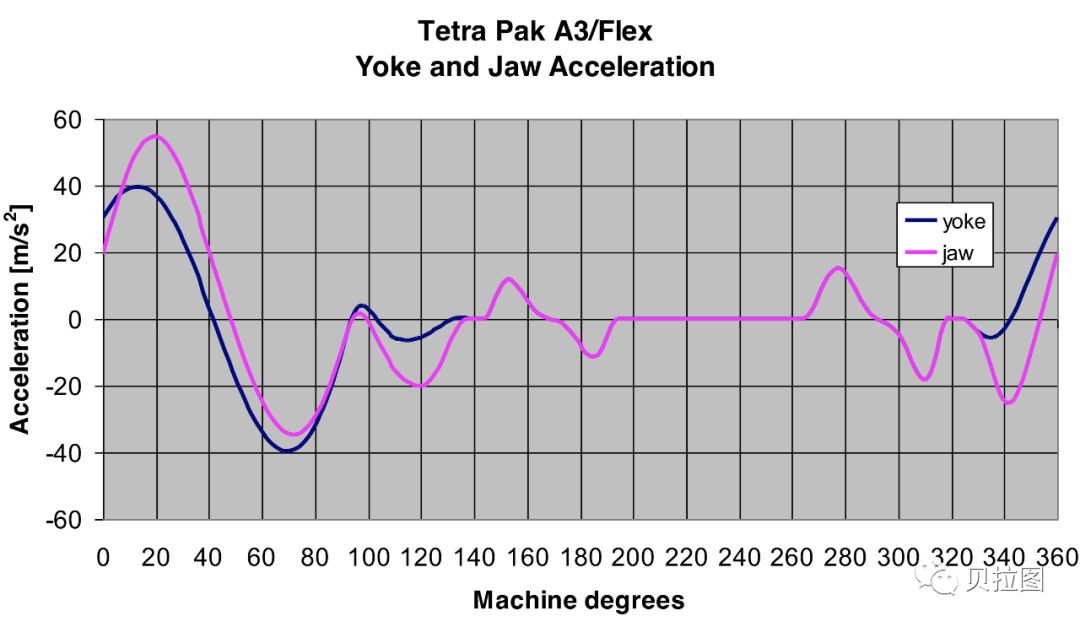
图 8: 利乐柔性机轭和爪的加速度曲线
以上两图,区别还是挺大的吧。